31 May Elastic Modulus
In Hooke’s Law (https://fea-solutions.co.uk/law-of-elasticity/), the Spring Constant k describes the relation between an applied load and the resulting deformation of a body.
It depends on both the shape (geometry) of the part as well as its material.
To have a constant that is just depending on the material but not on the geometry, Moduli of Elasticity have been defined. Depending on the direction of the applied load (and of the resulting stresses), a number of different elastic moduli are used, e.g. Shear Modulus (Modulus of Rigidity), Bending Modulus (Flexural Modulus) and Bulk Modulus.
The most important one is however the Young’s Modulus, because it is derived from Tensile Test results (https://fea-solutions.co.uk/tensile-tests/), which are the most common tests to determine mechanical material properties.
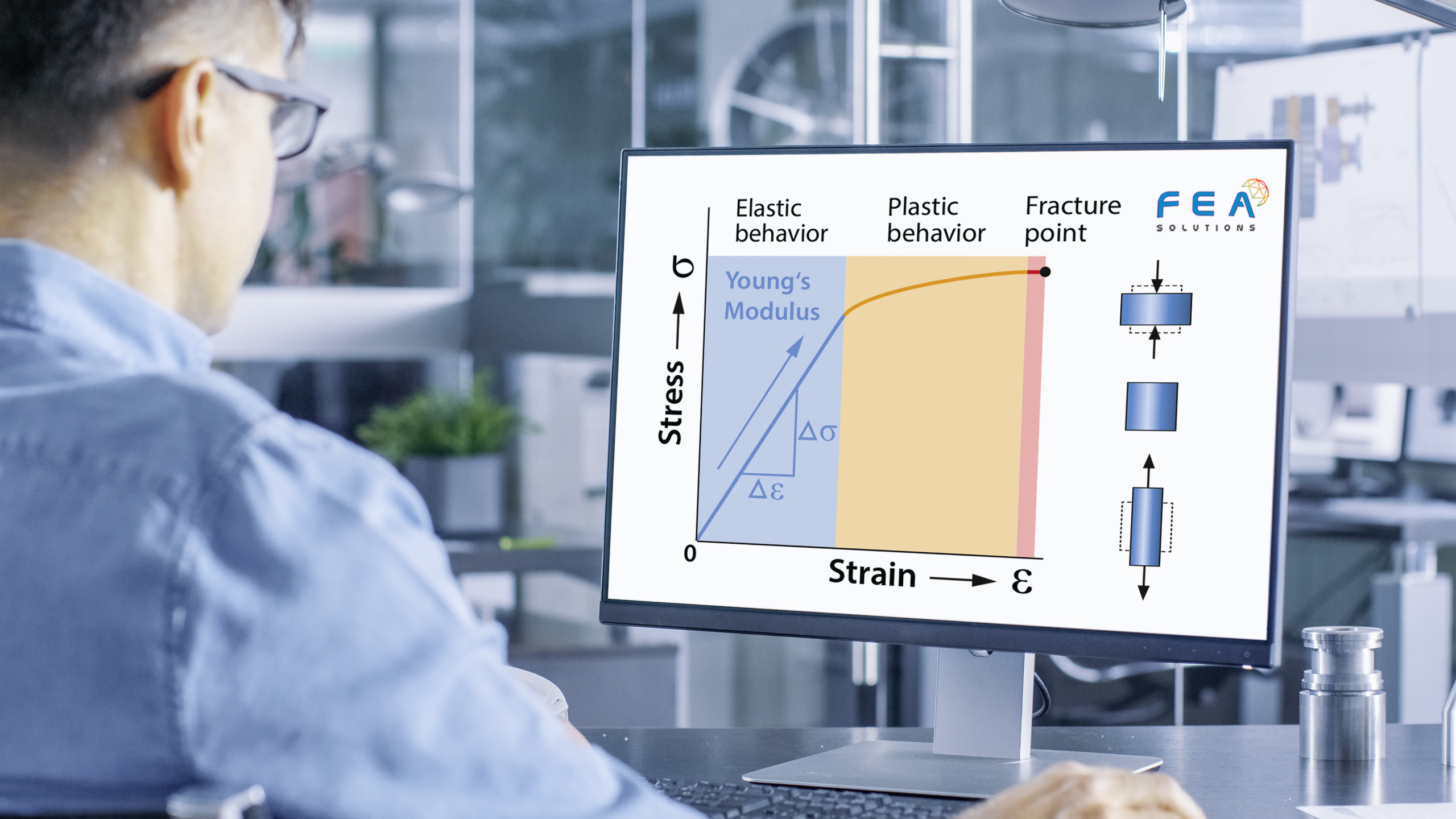
The Young’s Modulus is abbreviated with the letter E and is defined as the ratio between Stress and Strain. It is only valid in the linear-elastic region of the stress-strain curve. (https://fea-solutions.co.uk/elasticity-and-plasticity/)
Being the ratio between Stress and Strain means that the Young’s Modulus is the slope of the stress-strain curve (https://fea-solutions.co.uk/stress-strain-curves/).
Stiff materials have high Elastic Moduli, whereas flexible materials have low Elastic Moduli.
Typical values for the Young’s Modulus of common engineering materials are:
Steel 200,000MPa
Titanium 110,000MPa
Aluminium 70,000MPa
Plastics 3,000MPa (very much dependent on type of plastic)
It should be noted that although all steel grades for example have very similar Young’s Moduli, their Strength (e.g. Yield Limit) might be very different. However, in the most common FEA application, which is linear-elastic stress analysis, only the Young’s Modulus is an input value, but the Strength is not. Hence, even if is later decided to change a material grade, the FEA results will still be valid (as long as the resulting stresses are below the Yield Strength).
If you have further questions, please call us today on 01202 798991.
