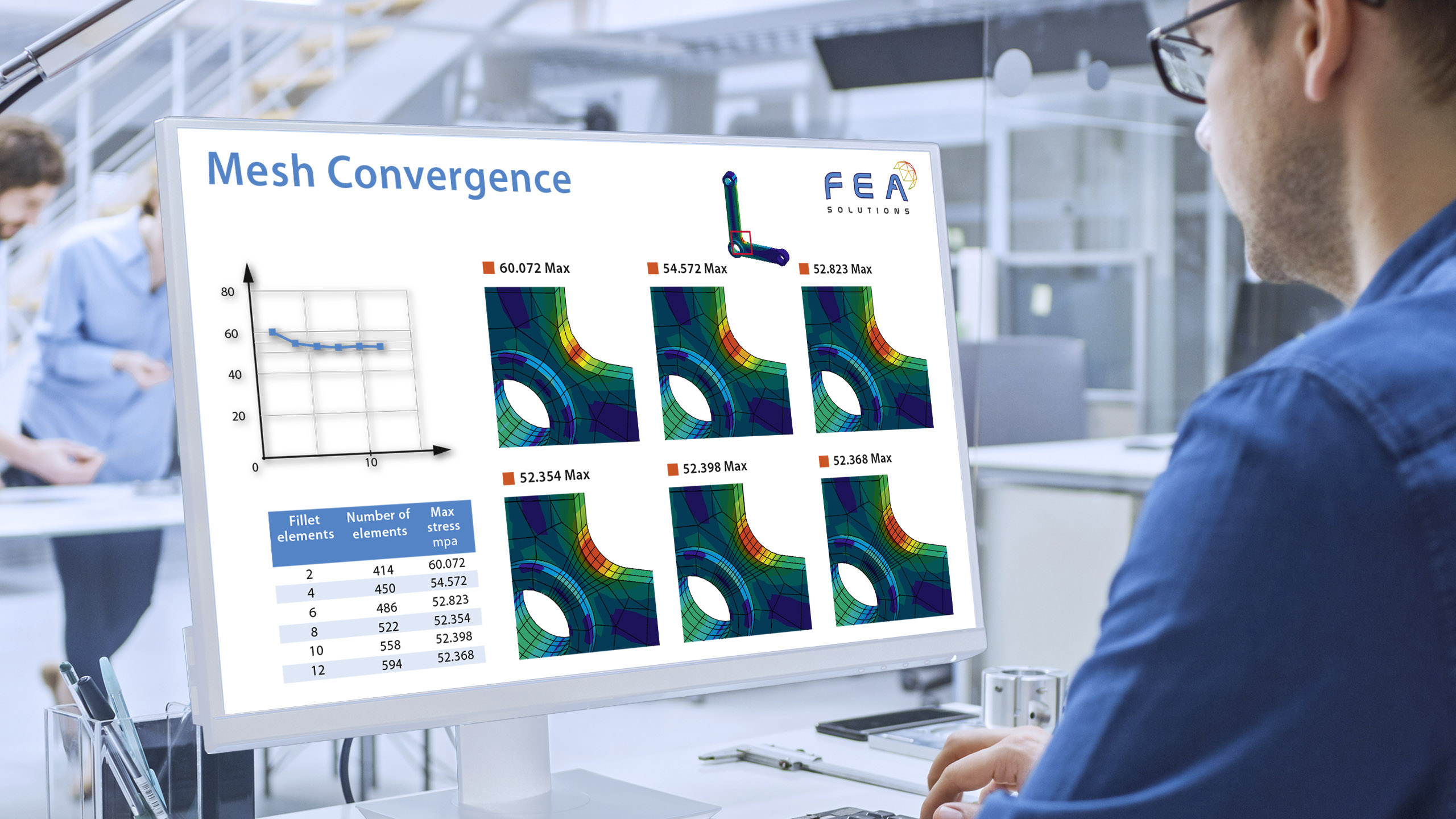
25 May Mesh Convergence
When referring to convergence in FEA, it could mean one of two things:
– Mesh Convergence
– Analysis Convergence (https://fea-solutions.co.uk/analysis-convergence/)
Mesh convergence determines how many elements are needed in a model so that the FEA results, in particular the peak stresses, are not affected by further refining the mesh (https://fea-solutions.co.uk/fea-terminology/).
In a mesh convergence study, the mesh is refined in steps. After each refinement step, the analysis is re-run and the peak stress result and the number of elements are recorded. These are then plotted against each other and a point should be observable where the results converge. This convergence point is dictated by various engineering standards. For example DNVGL-RP-F112 appendix A.1 states that for a linear analysis (https://fea-solutions.co.uk/elasticity-and-plasticity/), convergence is reached with a 3% convergence error on stress, when a halving of local element size is applied. For a non-linear analysis (https://fea-solutions.co.uk/non-linear-behaviour/), this convergence error is 5% on total strain. Although peak stresses usually increase to a convergence value with increased mesh density, they can also decrease to this value.
It is good practice to increase the mesh density only in areas of high stress gradient rather than throughout the FEA model.
Please call us today on +44 (0)1202 798991 for any engineering analysis requirements you might have.
