21 Feb Modal Analysis
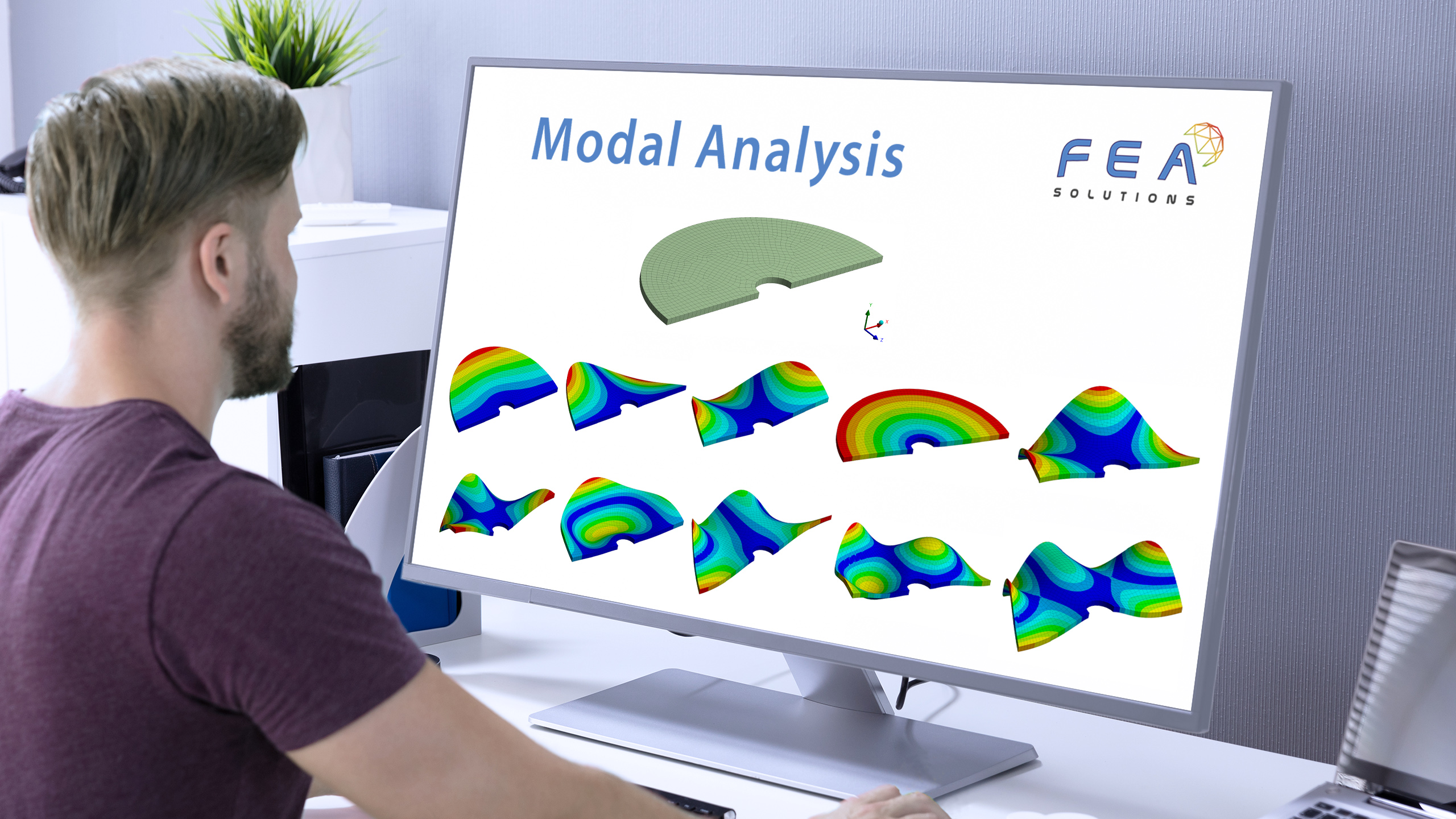
Modal Analyses are used to find the natural frequencies and their associated modes (deformation shapes) of a structure.
The natural frequency is the frequency at which a system vibrates in the absence of external excitations. Modal Analysis automatically applies unit loads, which can’t be adjusted by the FEA engineer. Therefore the magnitude of the results such as displacements and stresses are for this unit load only and should not be used to determine if a structure is safe or not. This can only be determined when the dynamic excitations are applied as well, which is done in separate analyses. In spite of this, modal analysis results provide an important insight into the dynamic behaviour of a structure and are often recommended in addition to static stress analyses.
The mode shapes are the specific patterns of vibration that occur in a system at a specific natural frequency. Each natural frequency has its own unique mode shape. However mode shapes of different frequencies can appear similar.
The natural frequencies of a system are different if the structure is unstressed or stressed. Tensile stresses increase the natural frequencies, compressive stresses reduce them. A commonly used example is the string of a guitar: tightening it will increase the tone, which is the audible expression of its frequency.
Modal Analysis is a purely linear analysis. Any non-linearities that might exist in the actual structure cannot be represented. A mathematical model for a non-linear modal analysis does not exist. For more information on non-linear behaviour, please look at our blog: https://fea-solutions.co.uk/non-linear-behaviour/ . Due to this purely linear analysis, any further analysis completed using the results of a modal analysis, such as a Modal Superposition analysis, are also considered purely linear analysis.
Please call us today on +44 (0)1202 798991 for any engineering analysis requirements you might have.
